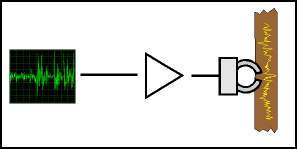
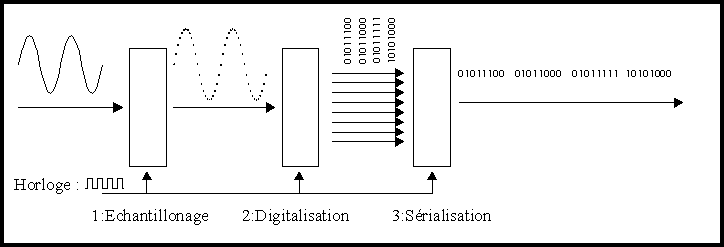
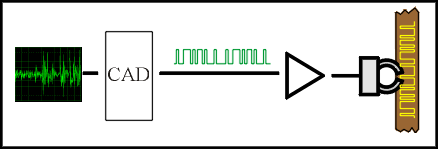
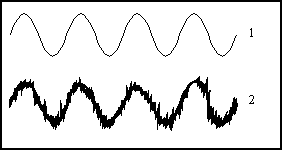
La première étape est l'échantillonnage.
A des intervalles de temps définis par l'horloge
on mesure la tension présente à l'entrée du circuit.
C'est à dire que pendant un bref instant on prend "une photo" de
la valeur du signal d'entrée qui, lui, continue de varier linéairement.
Tout se passe donc comme si l'échantillonnage découpait
le signal d'entrée en "tranches".
Cette étape d'échantillonnage peut se faire pendant le front
montant de l'horloge et son palier supérieur.
La seconde étape va consister à digitaliser
l'échantillon. Le digitaliseur va convertir la tension présente
à son entrée en un mot binaire sur 4, 8, 10, 16 ... bits
suivant la qualité désirée.
Dans l'exemple précédant le mot sera de 8 bits (1 octet)
et aura pour fourchette de valeurs : 00000000 (0) à 11111111
(255). Il faut bien sûr que le signal d'entrée soit "adapté"
au digitaliseur. C'est à dire que par des réglages annexes
on calibre la valeur maximale du signal d'entrée pour
avoir en sortie 11111111. On peut décider, par exemple, que la
valeur 11111111 sera atteinte par un signal d'entrée de 2V. Il
faudra donc veiller à ce que le signal d'entrée ne dépasse
jamais 2V sous peine d'obtenir une conversion erronée.
A ce stade on peut faire deux remarques :
- Alors que le signal d'entrée analogique pouvait prendre
un nombre de valeurs infini entre 0 et 2V (par exemple 1V ou 1.01V
ou 1.2568974V...), le mot binaire de sortie n'en contiendra que 256
(0 représentant 0V et 255 représentant 2V)
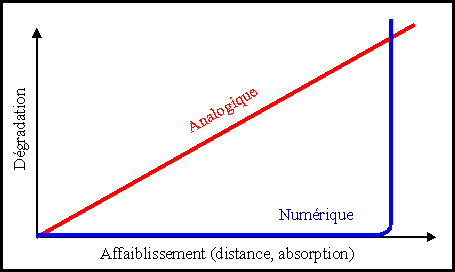
- L'information utile a changé de nature. Dans le signal analogique
d'entrée cette information était contenue dans l'amplitude
et la fréquence du signal électrique. Dans le mot binaire
de sortie l'information est un nombre complètement indépendant
de valeurs électriques. On peut décider que le "0" sera
défini pour une valeur électrique de 0V et le "1" par
une valeur de 5V. On peut aussi décider que le "0" le sera
pour une valeur de -12V et le "1" pour une valeur de +12V.
Plus intéressant encore, on peut décider que le "0" sera
défini pour une valeur comprise entre 0 et 2V et le "1" pour
une valeur de 3 à 5V.
La troisième étape, facultative, consiste à sérialiser
les mots binaires. 4, 8, 10 ou 16 fils, ce n'est pas toujours facile à
manipuler. Il est parfois préférable d'envoyer les bits
"à la queue leu leu" sur un seul fil. On peut remarquer que la
fréquence d'envoi des bits sur ce fil unique sera 8 fois plus grande
que la fréquence d'échantillonnage (dans le cas d'un convertisseur
8 bits) : En effet chaque coup d'horloge génère un mot de
8 bits sur 8 fils. Il faut donc que pendant ce même intervalle de
temps les 8 bits générés par le coup d'horloge précédant
aient été envoyé sur le fil unique de sortie.
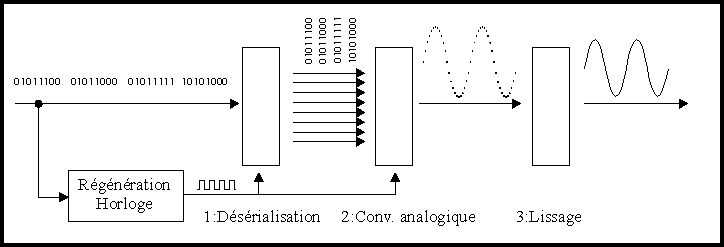
La figure ci-dessous illustre le processus inverse permettant, à
partir d'un train binaire, de retrouver le signal analogique.
|